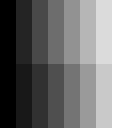Perception

Brightness Sensitivity

There are several ways to describe the sensitivity of the human visual system. To begin, let us assume that a homogeneous region in an image has an intensity as a function of wavelength (color) given by I( ). Further let us assume that I( ) = I_o, a constant.

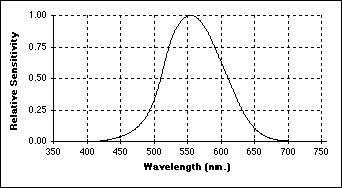
Wavelength sensitivity

The perceived intensity as a function of , the spectral sensitivity, for the "typical observer" is shown in Figure 10 .

Figure 10: Spectral Sensitivity of the "typical" human observer

Stimulus sensitivity

If the constant intensity (brightness) I_o is allowed to vary then, to a good approximation, the visual response, R, is proportional to the logarithm of the intensity. This is known as the Weber-Fechner law:

The implications of this are easy to illustrate. Equal perceived steps in brightness, R = k, require that the physical brightness (the stimulus) increases exponentially. This is illustrated in Figure 11ab.

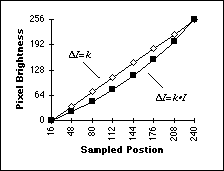
A horizontal line through the top portion of Figure 11a shows a linear increase in objective brightness (Figure 11b) but a logarithmic increase in subjective brightness. A horizontal line through the bottom portion of Figure 11a shows an exponential increase in objective brightness (Figure 11b) but a linear increase in subjective brightness.

Figure 11a Figure 11b (top) Brightness step I = k Actual brightnesses plus interpolated values (bottom) Brightness step I = k*I

The Mach band effect is visible in Figure 11a. Although the physical brightness is constant across each vertical stripe, the human observer perceives an "undershoot" and "overshoot" in brightness at what is physically a step edge. Thus, just before the step, we see a slight decrease in brightness compared to the true physical value. After the step we see a slight overshoot in brightness compared to the true physical value. The total effect is one of increased, local, perceived contrast at a step edge in brightness.

Spatial Frequency Sensitivity

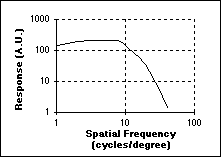
If the constant intensity (brightness) I_o is replaced by a sinusoidal grating with increasing spatial frequency (Figure 12a), it is possible to determine the spatial frequency sensitivity. The result is shown in Figure 12b .

Figure 12a Figure 12b Sinusoidal test grating Spatial frequency sensitivity

To translate these data into common terms, consider an "ideal" computer monitor at a viewing distance of 50 cm. The spatial frequency that will give maximum response is at 10 cycles per degree. (See Figure 12b.) The one degree at 50 cm translates to 50 tan(1deg.) = 0.87 cm on the computer screen. Thus the spatial frequency of maximum response f_max = 10 cycles/0.87 cm = 11.46 cycles/cm at this viewing distance. Translating this into a general formula gives:

where d = viewing distance measured in cm.

Color Sensitivity

uman color perception is an exceedingly complex topic. As such we can only present a brief introduction here. The physical perception of color is based upon three color pigments in the retina.

Standard observer

Based upon psychophysical measurements, standard curves have been adopted by the CIE (Commission Internationale de l'Eclairage) as the sensitivity curves for the "typical" observer for the three "pigments" . These are shown in Figure 13. These are not the actual pigment absorption characteristics found in the "standard" human retina but rather sensitivity curves derived from actual data .

Figure 13: Standard observer color sensitivity curves.

For an arbitrary homogeneous region in an image that has an intensity as a function of wavelength (color) given by I( ), the three responses are called the tristimulus values:

CIE chromaticity coordinates

The chromaticity coordinates which describe the perceived color information are defined as:

The red chromaticity coordinate is given by x and the green chromaticity coordinate by y. The tristimulus values are linear in I( ) and thus the absolute intensity information has been lost in the calculation of the chromaticity coordinates {x,y}. All color distributions, I( ), that appear to an observer as having the same color will have the same chromaticity coordinates.

If we use a tunable source of pure color (such as a dye laser), then the intensity can be modeled as I( ) = d( - _o) with d(*) as the impulse function. The collection of chromaticity coordinates {x,y} that will be generated by varying _o gives the CIE chromaticity triangle as shown in Figure 14.

Figure 14: Chromaticity diagram containing the CIE chromaticity triangle associated with pure spectral colors and the triangle associated with CRT phosphors.

Pure spectral colors are along the boundary of the chromaticity triangle. All other colors are inside the triangle. The chromaticity coordinates for some standard sources are given in Table 6.

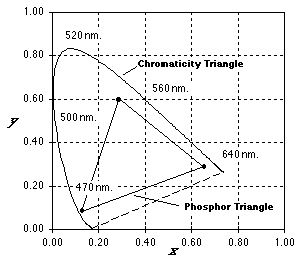
Table 6: Chromaticity coordinates for standard sources.

The description of color on the basis of chromaticity coordinates not only permits an analysis of color but provides a synthesis technique as well. Using a mixture of two color sources, it is possible to generate any of the colors along the line connecting their respective chromaticity coordinates. Since we cannot have a negative number of photons, this means the mixing coefficients must be positive. Using three color sources such as the red, green, and blue phosphors on CRT monitors leads to the set of colors defined by the interior of the "phosphor triangle" shown in Figure 14.

The formulas for converting from the tristimulus values (X,Y,Z) to the well-known CRT colors (R,G,B) and back are given by:

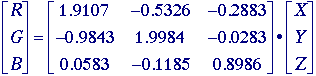
and

As long as the position of a desired color (X,Y,Z) is inside the phosphor triangle in Figure 14, the values of R, G, and B as computed by eq. will be positive and can therefore be used to drive a CRT monitor.

It is incorrect to assume that a small displacement anywhere in the chromaticity diagram (Figure 14) will produce a proportionally small change in the perceived color. An empirically-derived chromaticity space where this property is approximated is the (u',v') space:

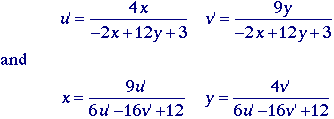
Small changes almost anywhere in the (u',v') chromaticity space produce equally small changes in the perceived colors.

 Optical Illusions

The description of the human visual system presented above is couched in standard engineering terms. This could lead one to conclude that there is sufficient knowledge of the human visual system to permit modeling the visual system with standard system analysis techniques. Two simple examples of optical illusions, shown in Figure 15, illustrate that this system approach would be a gross oversimplification. Such models should only be used with extreme care.

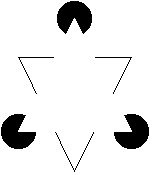
Figure 15: Optical Illusions

The left illusion induces the illusion of gray values in the eye that the brain "knows" does not exist. Further, there is a sense of dynamic change in the image due, in part, to the saccadic movements of the eye. The right illusion, Kanizsa's triangle, shows enhanced contrast and false contours neither of which can be explained by the system-oriented aspects of visual perception described above.