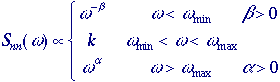Noise

While modern technology has made it possible to reduce the noise levels associated with various electro-optical devices to almost negligible levels, one noise source can never be eliminated and thus forms the limiting case when all other noise sources are "eliminated".

Photon Noise

When the physical signal that we observe is based upon light, then the quantum nature of light plays a significant role. A single photon at = 500 nm carries an energy of E = h = hc/ = 3.97 x 10^-19 Joules. Modern CCD cameras are sensitive enough to be able to count individual photons. (Camera sensitivity will be discussed in Section 7.2.) The noise problem arises from the fundamentally statistical nature of photon production. We cannot assume that, in a given pixel for two consecutive but independent observation intervals of length T, the same number of photons will be counted. Photon production is governed by the laws of quantum physics which restrict us to talking about an average number of photons within a given observation window. The probability distribution for p photons in an observation window of length T seconds is known to be Poisson:

where is the rate or intensity parameter measured in photons per second. It is critical to understand that even if there were no other noise sources in the imaging chain, the statistical fluctuations associated with photon counting over a finite time interval T would still lead to a finite signal-to-noise ratio (SNR). If we use the appropriate formula for the SNR (eq. ), then due to the fact that the average value and the standard deviation are given by:

Poisson process -

we have for the SNR:

Photon noise -

The three traditional assumptions about the relationship between signal and noise do not hold for photon noise:

* photon noise is not independent of the signal;

* photon noise is not Gaussian, and;

* photon noise is not additive.

For very bright signals, where T exceeds 10⁵, the noise fluctuations due to photon statistics can be ignored if the sensor has a sufficiently high saturation level. This will be discussed further in Section 7.3 and, in particular, eq. .

Thermal Noise

An additional, stochastic source of electrons in a CCD well is thermal energy. Electrons can be freed from the CCD material itself through thermal vibration and then, trapped in the CCD well, be indistinguishable from "true" photoelectrons. By cooling the CCD chip it is possible to reduce significantly the number of "thermal electrons" that give rise to thermal noise or dark current. As the integration time T increases, the number of thermal electrons increases. The probability distribution of thermal electrons is also a Poisson process where the rate parameter is an increasing function of temperature. There are alternative techniques (to cooling) for suppressing dark current and these usually involve estimating the average dark current for the given integration time and then subtracting this value from the CCD pixel values before the A/D converter. While this does reduce the dark current average, it does not reduce the dark current standard deviation and it also reduces the possible dynamic range of the signal.

On-chip Electronic Noise

This noise originates in the process of reading the signal from the sensor, in this case through the field effect transistor (FET) of a CCD chip. The general form of the power spectral density of readout noise is:

Readout noise -

where a and are constants and is the (radial) frequency at which the signal is transferred from the CCD chip to the "outside world." At very low readout rates ( < _min) the noise has a 1/f character. Readout noise can be reduced to manageable levels by appropriate readout rates and proper electronics. At very low signal levels (see eq. ), however, readout noise can still become a significant component in the overall SNR .

KTC Noise

Noise associated with the gate capacitor of an FET is termed KTC noise and can be non-negligible. The output RMS value of this noise voltage is given by:

KTC noise (voltage) -

where C is the FET gate switch capacitance, k is Boltzmann's constant, and T is the absolute temperature of the CCD chip measured in K. Using the relationships , the output RMS value of the KTC noise expressed in terms of the number of photoelectrons ( ) is given by:

KTC noise (electrons) -

where e^- is the electron charge. For C = 0.5 pF and T = 233 K this gives . This value is a "one time" noise per pixel that occurs during signal readout and is thus independent of the integration time (see Sections 6.1 and 7.7). Proper electronic design that makes use, for example, of correlated double sampling and dual-slope integration can almost completely eliminate KTC noise .

Amplifier Noise

The standard model for this type of noise is additive, Gaussian, and independent of the signal. In modern well-designed electronics, amplifier noise is generally negligible. The most common exception to this is in color cameras where more amplification is used in the blue color channel than in the green channel or red channel leading to more noise in the blue channel. (See also Section 7.6.)

Quantization Noise

Quantization noise is inherent in the amplitude quantization process and occurs in the analog-to-digital converter, ADC. The noise is additive and independent of the signal when the number of levels L >= 16. This is equivalent to B >= 4 bits. (See Section 2.1.) For a signal that has been converted to electrical form and thus has a minimum and maximum electrical value, eq. is the appropriate formula for determining the SNR. If the ADC is adjusted so that 0 corresponds to the minimum electrical value and 2^B-1 corresponds to the maximum electrical value then:

Quantization noise -

For B >= 8 bits, this means a SNR >= 59 dB. Quantization noise can usually be ignored as the total SNR of a complete system is typically dominated by the smallest SNR. In CCD cameras this is photon noise.