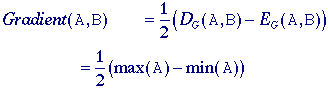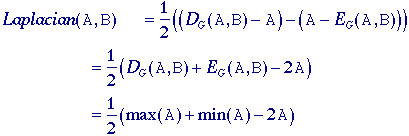Algorithms |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In this
Section we will describe operations that are fundamental to digital
image processing. These operations can be divided into four categories:
operations based on the image histogram, on simple mathematics, on
convolution, and on mathematical morphology. Further, these operations
can also be described in terms of their implementation as a point
operation, a local operation, or a global operation as described in
Section 2.2.1.
Histogram-based Operations
An important class of point operations is based upon the manipulation of an image histogram or a region histogram. The most important examples are described below. Contrast stretchingFrequently, an image is scanned in such a way that the resulting brightness values do not make full use of the available dynamic range. This can be easily observed in the histogram of the brightness values shown in Figure 6. By stretching the histogram over the available dynamic range we attempt to correct this situation. If the image is intended to go from brightness 0 to brightness 2B-1 (see Section 2.1), then one generally maps the 0% value (or minimum as defined in Section 3.5.2) to the value 0 and the 100% value (or maximum) to the value 2B-1. The appropriate transformation is given by: This
formula, however, can be somewhat sensitive to outliers and a less
sensitive and more general version is given by: In
this second version one might choose the 1% and 99% values for plow%
and phigh%, respectively, instead of the 0% and
100% values represented by eq. . It is also possible to apply the
contrast-stretching operation on a regional basis using the histogram
from a region to determine the appropriate limits for the algorithm.
Note that in eqs. and it is possible to suppress the term 2B-1
and simply normalize the brightness range to 0 <= b[m,n]
<= 1. This means representing the final pixel brightnesses as reals
instead of integers but modern computer speeds and RAM capacities make
this quite feasible. EqualizationWhen one wishes to compare two or more images on a specific basis, such as texture, it is common to first normalize their histograms to a "standard" histogram. This can be especially useful when the images have been acquired under different circumstances. The most common histogram normalization technique is histogram equalization where one attempts to change the histogram through the use of a function b = f (a) into a histogram that is constant for all brightness values. This would correspond to a brightness distribution where all values are equally probable. Unfortunately, for an arbitrary image, one can only approximate this result. For
a "suitable" function f (a) the relation between the
input probability density function, the output probability density
function, and the function f (a) is given by:
From
eq. we see that "suitable" means that f (a) is
differentiable and that df/da >= 0. For histogram equalization
we desire that pb(b) = constant and this means
that:
where
P(a) is the probability distribution function
defined in Section 3.5.1 and illustrated in Figure 6a. In other words,
the quantized probability distribution function normalized from 0
to 2B-1 is the look-up table required for histogram
equalization. Figures 21a-c illustrate the effect of contrast stretching
and histogram equalization on a standard image. The histogram
equalization procedure can also be applied on a regional basis.
Figure 21a Figure 21b Figure 21c Original Contrast Stretched istogram Equalized Other histogram-based operations
The histogram derived from a local region can also be used to drive local filters that are to be applied to that region. Examples include minimum filtering, median filtering, and maximum filtering . The concepts minimum, median, and maximum were introduced in Figure 6. The filters based on these concepts will be presented formally in Sections 9.4.2 and 9.6.10.
Mathematics-based OperationsWe
distinguish in this section between binary arithmetic and ordinary
arithmetic. In the binary case there are two brightness values
"0" and "1". In the ordinary case we begin with 2B
brightness values or levels but the processing of the image can easily
generate many more levels. For this reason many software systems
provide 16 or 32 bit representations for pixel brightnesses in order to
avoid problems with arithmetic overflow. Binary operations Operations based on binary (Boolean) arithmetic form the basis for a powerful set of tools that will be described here and extended in Section 9.6, mathematical morphology. The operations described below are point operations and thus admit a variety of efficient implementations including simple look-up tables. The standard notation for the basic set of binary operations is:
The
implication is that each operation is applied on a pixel-by-pixel basis.
For example,
These
operations are illustrated in Figure 22 where the binary value
"1" is shown in black and the value "0" in white.
c)
NOT(b) =
Figure 22: Examples of the various binary point operations. The
SUB(*) operation can be particularly useful when the image a
represents a region-of-interest that we want to analyze systematically
and the image b represents objects that, having been analyzed,
can now be discarded, that is subtracted, from the region. Arithmetic-based operationsThe gray-value point operations that form the basis for image processing are based on ordinary mathematics and include:
Convolution-based OperationsConvolution,
the mathematical, local operation defined in Section 3.1 is
central to modern image processing. The basic idea is that a window of
some finite size and shape--the support--is scanned across the
image. The output pixel value is the weighted sum of the input pixels
within the window where the weights are the values of the filter
assigned to every pixel of the window itself. The window with its
weights is called the convolution kernel. This leads
directly to the following variation on eq. . If the filter h[j,k]
is zero outside the (rectangular) window {j=0,1,...,J-1; k=0,1,...,K-1},
then, using eq. , the convolution can be written as the following finite
sum:
This
equation can be viewed as more than just a pragmatic mechanism for
smoothing or sharpening an image. Further, while eq. illustrates the
local character of this operation, eqs. and suggest that the operation
can be implemented through the use of the Fourier domain which requires
a global operation, the Fourier transform. Both of these aspects will be
discussed below. BackgroundIn a variety of image-forming
systems an appropriate model for the transformation of the physical
signal a(x,y) into an electronic signal c(x,y)
is the convolution of the input signal with the impulse response of the
sensor system. This system might consist of both an optical as well as
an electrical sub-system. If each of these systems can be treated as a
linear, shift-invariant (LSI) system then the convolution model
is appropriate. The definitions of these two, possible, system
properties are given below: Linearity
-
Shift-Invariance
-
where
w1 and w2 are arbitrary complex
constants and xo and yo are
coordinates corresponding to arbitrary spatial translations. Two
remarks are appropriate at this point. First, linearity implies (by
choosing w1 = w2 = 0) that
"zero in" gives "zero out". The offset described in
eq. means that such camera signals are not the output of a linear system
and thus (strictly speaking) the convolution result is not applicable.
Fortunately, it is straightforward to correct for this non-linear
effect. (See Section 10.1.) Second,
optical lenses with a magnification, M, other than 1x
are not shift invariant; a translation of 1 unit in the input image a(x,y)
produces a translation of M units in the output image c(x,y).
Due to the Fourier property described in eq. this case can still be
handled by linear system theory. If
an impulse point of light d(x,y) is imaged through an LSI
system then the impulse response of that system is called the point
spread function (PSF). The output image then
becomes the convolution of the input image with the PSF. The
Fourier transform of the PSF is called the optical transfer
function (OTF). For optical systems that are
circularly-symmetric, aberration-free, and diffraction-limited the PSF
is given by the Airy disk shown in Table 4-T.5. The OTF of the
Airy disk is also presented in Table 4-T.5. If
the convolution window is not the diffraction-limited PSF of the lens
but rather the effect of defocusing a lens then an appropriate model for
h(x,y) is a pill box of radius a as
described in Table 4-T.3. The effect on a test pattern is illustrated in
Figure 23.
Figure 23:
Convolution of test pattern with a pill box of radius a=4.5
pixels. The
effect of the defocusing is more than just simple blurring or smoothing.
The almost periodic negative lobes in the transfer function in
Table 4-T.3 produce a 180deg. phase shift in which black turns to white and vice-versa. The phase
shift is clearly visible in Figure 23b. Convolution in the spatial domain
In describing filters based on
convolution we will use the following convention. Given a filter h[j,k]
of dimensions J x K, we will
consider the coordinate [j=0,k=0] to be in the center of
the filter matrix, h. This is illustrated in Figure 24. The
"center" is well-defined when J and K are odd;
for the case where they are even, we will use the approximations (J/2,
K/2) for the "center" of the matrix.
Figure 24:
Coordinate system for describing h[j,k] When
we examine the convolution sum (eq. ) closely, several issues become
evident. *
Evaluation of formula for m=n=0 while rewriting the limits
of the convolution sum based on the "centering" of h[j,k]
shows that values of a[j,k] can be required that
are outside the image boundaries:
The
question arises - what values should we assign to the image a[m,n]
for m<0, m>=M, n<0, and n>=N?
There is no "answer" to this question. There are only
alternatives among which we are free to choose assuming we understand
the possible consequences of our choice. The standard alternatives are
a) extend the images with a constant (possibly zero) brightness value,
b) extend the image periodically, c) extend the image by mirroring it at
its boundaries, or d) extend the values at the boundaries indefinitely.
These alternatives are illustrated in Figure 25.
(a)
(b) (c) (d) Figure
25:
Examples of various alternatives to extend an image outside its formal
boundaries. See text for explanation. *
When the convolution sum is written in the standard form (eq. ) for an
image a[m,n] of size M x N:
we
see that the convolution kernel h[j,k] is mirrored
around j=k=0 to produce *
The computational complexity for a K x
K convolution kernel implemented in the spatial domain on an
image of N x
N is O(K2) where the complexity is
measured per pixel on the basis of the number of
multiplies-and-adds (MADDs). *
The value computed by a convolution that begins with integer
brightnesses for a[m,n] may produce a rational
number or a floating point number in the result c[m,n].
Working exclusively with integer brightness values will, therefore,
cause roundoff errors. *
Inspection of eq. reveals another possibility for efficient
implementation of convolution. If the convolution kernel h[j,k]
is separable, that is, if the kernel can be written as:
then
the filtering can be performed as follows:
This
means that instead of applying one, two-dimensional filter it is
possible to apply two, one-dimensional filters, the first one in the k
direction and the second one in the j direction. For an N x
N image this, in general, reduces the computational complexity
per pixel from O(J* K) to O(J+K). An
alternative way of writing separability is to note that the convolution
kernel (Figure 24) is a matrix h and, if separable, h can
be written as:
where
"t" denotes the matrix transpose operation.
In other words, h can be expressed as the outer product
of a column vector [hcol] and a row vector [hrow].
*
For certain filters it is possible to find an incremental implementation
for a convolution. As the convolution window moves over the image (see
eq. ), the leftmost column of image data under the window is shifted out
as a new column of image data is shifted in from the right. Efficient
algorithms can take advantage of this and, when combined with separable
filters as described above, this can lead to algorithms where the
computational complexity per pixel is O(constant). Convolution in the frequency domain
In Section 3.4 we indicated that
there was an alternative method to implement the filtering of images
through convolution. Based on eq. it appears possible to achieve the
same result as in eq. by the following sequence of operations: i)
Compute A(
ii)
Multiply A(
iii)
Compute the result c[m,n] = F-1{A(
*
While it might seem that the "recipe" given above in eq.
circumvents the problems associated with direct convolution in the
spatial domain--specifically, determining values for the image outside
the boundaries of the image--the Fourier domain approach, in fact,
simply "assumes" that the image is repeated periodically
outside its boundaries as illustrated in Figure 25b. This phenomenon is
referred to as circular convolution. If
circular convolution is not acceptable then the other possibilities
illustrated in Figure 25 can be realized by embedding the image a[m,n]
and the filter (
*
The computational complexity per pixel of the Fourier approach for an
image of N x
N and for a convolution kernel of K x
K is O(logN) complex MADDs independent
of K. ere we assume that N > K and that N
is a highly composite number such as a power of two. (See also 2.1.)
This latter assumption permits use of the computationally-efficient Fast
Fourier Transform (FFT) algorithm. Surprisingly then, the
indirect route described by eq. can be faster than the direct route
given in eq. . This requires, in general, that K2
>> logN. The range of K and N for which this
holds depends on the specifics of the implementation. For the machine on
which this manuscript is being written and the specific image processing
package that is being used, for an image of N = 256 the Fourier
approach is faster than the convolution approach when K >= 15.
(It should be noted that in this comparison the direct convolution
involves only integer arithmetic while the Fourier domain approach
requires complex floating point arithmetic.)
Smoothing Operations
These
algorithms are applied in order to reduce noise and/or to prepare images
for further processing such as segmentation. We distinguish between
linear and non- linear algorithms where the former are amenable to
analysis in the Fourier domain and the latter are not. We also
distinguish between implementations based on a rectangular support for
the filter and implementations based on a circular support for the
filter. Linear Filters
Several filtering algorithms
will be presented together with the most useful supports. *
Uniform filter - The output image is based on a local averaging
of the input filter where all of the values within the filter support
have the same weight. In the continuous spatial domain (x,y)
the PSF and transfer function are given in Table 4-T.1 for
the rectangular case and in Table 4-T.3 for the circular (pill box)
case. For the discrete spatial domain [m,n] the filter
values are the samples of the continuous domain case. Examples for the
rectangular case (J=K=5) and the circular case (R=2.5)
are shown in Figure 26.
Figure 26:
Uniform filters for image smoothing Note
that in both cases the filter is normalized so that
*
Triangular filter - The output image is based on a local
averaging of the input filter where the values within the filter support
have differing weights. In general, the filter can be seen as the
convolution of two (identical) uniform filters either rectangular or
circular and this has direct consequences for the computational
complexity . (See Table 13.) In the continuous spatial domain the PSF
and transfer function are given in Table 4-T.2 for the
rectangular support case and in Table 4-T.4 for the circular (pill box)
support case. As seen in Table 4 the transfer functions of these
filters do not have negative lobes and thus do not exhibit phase
reversal. Examples
for the rectangular support case (J=K=5) and the circular
support case (R=2.5) are shown in Figure 27. The filter is again
normalized so that
(a)
Pyramidal filter (J=K=5) (b) Cone filter (R=2.5)
Figure 27:
Triangular filters for image smoothing *
Gaussian filter - The use of the Gaussian kernel for smoothing
has become extremely popular. This has to do with certain properties of
the Gaussian (e.g. the central limit theorem, minimum space-bandwidth
product) as well as several application areas such as edge finding and
scale space analysis. The PSF and transfer function for
the continuous space Gaussian are given in Table 4-T6. The Gaussian
filter is separable:
There
are four distinct ways to implement the Gaussian: -
Convolution using a finite number of samples (No) of
the Gaussian as the convolution kernel. It is common to choose No
=
-
Repetitive convolution using a uniform filter as the convolution kernel.
The
actual implementation (in each dimension) is usually of the form:
This
implementation makes use of the approximation afforded by the central
limit theorem. For a desired
-
Multiplication in the frequency domain. As the Fourier transform of a
Gaussian is a Gaussian (see Table -T.6), this means that it is
straightforward to prepare a filter (
-
Use of a recursive filter implementation. A recursive filter has an
infinite impulse response and thus an infinite support. The separable
Gaussian filter can also be implemented by applying the following recipe
in each dimension when
i)
Choose the
The
relation between the desired
The
filter coefficients {b0,b1,b2,b3,B}
are defined by:
The
one-dimensional forward difference equation takes an input row
(or column) a[n] and produces an intermediate output
result w[n] given by:
The
one-dimensional backward difference equation takes
the intermediate result w[n] and produces the output c[n]
given by:
The
forward equation is applied from n = 0 up to n = N
- 1 while the backward equation is applied from n = N
- 1 down to n = 0. The
relative performance of these various implementation of the Gaussian
filter can be described as follows. Using the root-square error
The
root-square error measure is extremely conservative and thus all
filters, with the exception of "Uniform 3x"
for large
a)
Accuracy comparison b) Speed comparison Figure
28:
Comparison of various Gaussian algorithms with N=256. The legend
is spread across both graphs *
Other - The Fourier domain approach offers the opportunity to
implement a variety of smoothing algorithms. The smoothing filters will
then be lowpass filters. In general it is desirable to use
a lowpass filter that has zero phase so as not to produce phase
distortion when filtering the image. The importance of phase was
illustrated in Figures 5 and 23. When the frequency domain
characteristics can be represented in an analytic form, then this can
lead to relatively straightforward implementations of (
Non-Linear Filters
A variety of smoothing filters
have been developed that are not linear. While they cannot, in general,
be submitted to Fourier analysis, their properties and domains of
application have been studied extensively. *
Median filter - The median statistic was described in Section
3.5.2. A median filter is based upon moving a window over an image (as
in a convolution) and computing the output pixel as the median value of
the brightnesses within the input window. If the window is J x
K in size we can order the J*K pixels in brightness
value from smallest to largest. If J*K is odd then the
median will be the (J*K+1)/2 entry in the list of ordered
brightnesses. Note that the value selected will be exactly equal to one
of the existing brightnesses so that no roundoff error will be involved
if we want to work exclusively with integer brightness values. The
algorithm as it is described above has a generic complexity per pixel of
O(J*K*log(J*K)). Fortunately, a fast
algorithm (due to uang et al. ) exists that reduces the complexity to O(K)
assuming J >= K. A
useful variation on the theme of the median filter is the percentile
filter. ere the center pixel in the window is replaced not by the
50% (median) brightness value but rather by the p% brightness
value where p% ranges from 0% (the minimum filter)
to 100% (the maximum filter). Values other then (p=50)%
do not, in general, correspond to smoothing filters. *
Kuwahara filter - Edges play an important role in our perception
of images (see Figure 15) as well as in the analysis of images. As such
it is important to be able to smooth images without disturbing the
sharpness and, if possible, the position of edges. A filter that
accomplishes this goal is termed an edge-preserving filter
and one particular example is the Kuwahara filter . Although this filter
can be implemented for a variety of different window shapes, the
algorithm will be described for a square window of size J = K
= 4L + 1 where L is an integer. The window is partitioned
into four regions as shown in Figure 29.
Figure 29:
Four, square regions defined for the Kuwahara filter. In this example L=1
and thus J=K=5. Each region is [(J+1)/2] x
[(K+1)/2]. In
each of the four regions (i=1,2,3,4), the mean brightness, mi
in eq. , and the variancei, si2
in eq. , are measured. The output value of the center pixel in the
window is the mean value of that region that has the smallest variance. Summary of Smoothing Algorithms
The following table summarizes
the various properties of the smoothing algorithms presented above. The
filter size is assumed to be bounded by a rectangle of J x
K where, without loss of generality, J >= K. The
image size is N x N.
Table
13: Characteristics of smoothing filters.
ªSee text for additional explanation. Examples
of the effect of various smoothing algorithms are shown in Figure 30.
a)
Original b) Uniform 5 x
5 c) Gaussian (
Figure 30:
Illustration of various linear and non-linear smoothing filters
Derivative-based Operations
Just
as smoothing is a fundamental operation in image processing so is the
ability to take one or more spatial derivatives of the image. The
fundamental problem is that, according to the mathematical definition of
a derivative, this cannot be done. A digitized image is not a continuous
function a(x,y) of the spatial variables but rather
a discrete function a[m,n] of the integer spatial
coordinates. As a result the algorithms we will present can only be seen
as approximations to the true spatial derivatives of the original
spatially-continuous image. Further,
as we can see from the Fourier property in eq. , taking a derivative
multiplies the signal spectrum by either u or v. This
means that high frequency noise will be emphasized in the resulting
image. The general solution to this problem is to combine the derivative
operation with one that suppresses high frequency noise, in short,
smoothing in combination with the desired derivative operation. First Derivatives
As an image is a function of two
(or more) variables it is necessary to define the direction in which the
derivative is taken. For the two-dimensional case we have the horizontal
direction, the vertical direction, or an arbitrary direction which can
be considered as a combination of the two. If we use hx
to denote a horizontal derivative filter (matrix), hy
to denote a vertical derivative filter (matrix), and h
*
Gradient filters - It is also possible to generate a vector
derivative description as the gradient,
where
Gradient
magnitude -
and
Gradient
direction -
The
gradient magnitude is sometimes approximated by: Approx.
Gradient magnitude -
The
final results of these calculations depend strongly on the choices of hx
and hy. A number of possible choices for (hx,
hy) will now be described. *
Basic derivative filters - These filters are specified by:
where
"t" denotes matrix transpose. These two
filters differ significantly in their Fourier magnitude and Fourier
phase characteristics. For the frequency range 0 <=
The
second form (ii) gives suppression of high frequency terms (
*
Prewitt gradient filters - These filters are specified by:
Both
hx and hy are separable. Beyond the
computational implications are the implications for the analysis of the
filter. Each filter takes the derivative in one direction using eq. ii
and smoothes in the orthogonal direction using a one-dimensional version
of a uniform filter as described in Section 9.4.1. *
Sobel gradient filters - These filters are specified by:
Again,
hx and hy are separable. Each filter
takes the derivative in one direction using eq. ii and smoothes
in the orthogonal direction using a one-dimensional version of a triangular
filter as described in Section 9.4.1. *
Alternative gradient filters - The variety of techniques
available from one-dimensional signal processing for the design of
digital filters offers us powerful tools for designing one-dimensional
versions of hx and hy. Using the
Parks-McClellan filter design algorithm, for example, we can choose the
frequency bands where we want the derivative to be taken and the
frequency bands where we want the noise to be suppressed. The algorithm
will then produce a real, odd filter with a minimum length that meets
the specifications. As
an example, if we want a filter that has derivative characteristics in a
passband (with weight 1.0) in the frequency range 0.0 <=
The
gradient can then be calculated as in eq. . *
Gaussian gradient filters - In modern digital image processing
one of the most common techniques is to use a Gaussian filter (see
Section 9.4.1) to accomplish the required smoothing and one of the
derivatives listed in eq. . Thus, we might first apply the recursive
Gaussian in eq. followed by eq. ii to achieve the desired,
smoothed derivative filters hx and hy.
Further, for computational efficiency, we can combine these two steps
as:
where
the various coefficients are defined in eq. . The first (forward)
equation is applied from n = 0 up to n = N -
1 while the second (backward) equation is applied from n = N
- 1 down to n = 0. *
Summary - Examples of the effect of various derivative algorithms
on a noisy version of Figure 30a (SNR = 29 dB) are shown in
Figure 31a-c. The effect of various magnitude gradient algorithms
on Figure 30a are shown in Figure 32a-c. After processing, all images
are contrast stretched as in eq. for display purposes.
(a)
(b) (c) Simple Derivative - eq. ii
Sobel - eq. Gaussian (
Figure 31:
Application of various algorithms for hx - the
horizontal derivative.
(a)
(b) (c) Simple Derivative - eq. ii
Sobel - eq. Gaussian (
Figure 32:
Various algorithms for the magnitude gradient, |
The
magnitude gradient takes on large values where there are strong edges in
the image. Appropriate choice of
Second Derivatives
It is, of course, possible to
compute higher-order derivatives of functions of two variables. In image
processing, as we shall see in Sections 10.2.1 and 10.3.2, the second
derivatives or Laplacian play an important role. The Laplacian is
defined as:
where
h2x and h2y are second derivative
filters. In the frequency domain we have for the Laplacian filter (from
eq. ):
The
transfer function of a Laplacian corresponds to a parabola (u,v)
= -(u2 + v2). *
Basic second derivative filter - This filter is specified by:
and
the frequency spectrum of this filter, in each direction, is given by:
over
the frequency range -
and
used as in eq. . *
Frequency domain Laplacian - This filter is the implementation of
the general recipe given in eq. and for the Laplacian filter takes the
form:
*
Gaussian second derivative filter - This is the straightforward
extension of the Gaussian first derivative filter described above and
can be applied independently in each dimension. We first apply Gaussian
smoothing with a
For
efficiency, we can use the recursive implementation and combine the two
steps--smoothing and derivative operation--as follows:
where
the various coefficients are defined in eq. . Again, the first (forward)
equation is applied from n = 0 up to n = N -
1 while the second (backward) equation is applied from n = N
- 1 down to n = 0. *
Alternative Laplacian filters - Again one-dimensional digital
filter design techniques offer us powerful methods to create filters
that are optimized for a specific problem. Using the Parks-McClellan
design algorithm, we can choose the frequency bands where we want the
second derivative to be taken and the frequency bands where we want the
noise to be suppressed. The algorithm will then produce a real, even
filter with a minimum length that meets the specifications. As
an example, if we want a filter that has second derivative
characteristics in a passband (with weight 1.0) in the frequency range
0.0 <=
The
Laplacian can then be calculated as in eq. . *
SDGD filter - A filter that is especially useful in edge finding
and object measurement is the Second-Derivative-in-the-Gradient-Direction
(SDGD) filter. This filter uses five partial derivatives:
Note
that Axy = Ayx which accounts for
the five derivatives. This
SDGD combines the different partial derivatives as follows:
As
one might expect, the large number of derivatives involved in this
filter implies that noise suppression is important and that Gaussian
derivative filters--both first and second order--are highly recommended
if not required . It is also necessary that the first and second
derivative filters have essentially the same passbands and stopbands.
This means that if the first derivative filter h1x is
given by [1 0 -1] (eq. ii) then the second derivative filter
should be given by h1x
*
Summary - The effects of the various second derivative filters are illustrated
in Figure 33a-e. All images were contrast stretched for display purposes
using eq. and the parameters 1% and 99%.
(a)
(b) (c) Laplacian - eq. Fourier parabola -
eq. Gaussian (
Figure 33:
Various algorithms for the Laplacian and Laplacian-related filters. Other Filters
An infinite number of filters,
both linear and non-linear, are possible for image processing. It is
therefore impossible to describe more than the basic types in this
section. The description of others can be found be in the reference
literature (see Section 11) as well as in the applications literature.
It is important to use a small consistent set of test images that are
relevant to the application area to understand the effect of a given
filter or class of filters. The effect of filters on images can be
frequently understood by the use of images that have pronounced regions
of varying sizes to visualize the effect on edges or by the use of test
patterns such as sinusoidal sweeps to visualize the effects in the
frequency domain. The former have been used above (Figures 21, 23, and
30-33) and the latter are demonstrated below in Figure 34.
(a)
Lowpass filter (b) Bandpass filter
(c) ighpass filter Figure 34:
Various convolution algorithms applied to sinusoidal test image.
Morphology-based Operations
In
Section 1 we defined an image as an (amplitude) function of two, real
(coordinate) variables a(x,y) or two, discrete
variables a[m,n]. An alternative definition of an
image can be based on the notion that an image consists of a set (or
collection) of either continuous or discrete coordinates. In a sense the
set corresponds to the points or pixels that belong to the objects in
the image. This is illustrated in Figure 35 which contains two objects
or sets A and B. Note that the coordinate
system is required. For the moment we will consider the pixel values to
be binary as discussed in Section 2.1 and 9.2.1. Further we shall
restrict our discussion to discrete space (Z2). More
general discussions can be found in .
Figure 35:
A binary image containing two object sets A and B.
The
object A consists of those pixels a
that share some common property: Object
-
As
an example, object B in Figure 35 consists of {[0,0],
[1,0], [0,1]}. The
background of A is given by Ac
(the complement of A) which is defined as those
elements that are not in A: Background
-
In
Figure 3 we introduced the concept of neighborhood connectivity. We now
observe that if an object A is defined on the basis of C-connectivity
(C=4, 6, or 8) then the background Ac
has a connectivity given by 12 - C. The necessity for this is
illustrated for the Cartesian grid in Figure 36.
Figure 36:
A binary image requiring careful definition of object and background
connectivity. Fundamental definitions
The fundamental operations
associated with an object are the standard set operations union, intersection,
and complement {
*
Translation - Given a vector x and a set A, the translation,
A + x, is defined as:
Note
that, since we are dealing with a digital image composed of pixels at
integer coordinate positions (Z2), this implies
restrictions on the allowable translation vectors x. The
basic Minkowski set operations--addition and
subtraction--can now be defined. First we note that the individual
elements that comprise B are not only pixels but also vectors
as they have a clear coordinate position with respect to [0,0]. Given
two sets A and B: Minkowski
addition -
Minkowski
subtraction -
Dilation and Erosion
From these two Minkowski
operations we define the fundamental mathematical morphology operations dilation
and erosion: Dilation
-
Erosion
-
where
(a)
Dilation D(A,B) (b) Erosion E(A,B) Figure
37:
A binary image containing two object sets A and B.
The three pixels in B are "color-coded" as is
their effect in the result. While
either set A or B can be thought of as an
"image", A is usually considered as the image
and B is called a structuring element. The
structuring element is to mathematical morphology what the convolution
kernel is to linear filter theory. Dilation,
in general, causes objects to dilate or grow in size; erosion
causes objects to shrink. The amount and the way that they grow or
shrink depend upon the choice of the structuring element. Dilating or
eroding without specifying the structural element makes no more sense
than trying to lowpass filter an image without specifying the filter.
The two most common structuring elements (given a Cartesian grid) are
the 4-connected and 8-connected sets, N4 and N8.
They are illustrated in Figure 38.
(a)
N4
(b) N8
Figure 38:
The standard structuring elements N4 and N8.
Dilation
and erosion have the following properties: Commutative
-
Non-Commutative
-
Associative
-
Translation
Invariance -
Duality
-
With
A as an object and Ac as
the background, eq. says that the dilation of an object is
equivalent to the erosion of the background. Likewise, the erosion
of the object is equivalent to the dilation of the background. Except
for special cases: Non-Inverses
-
Erosion
has the following translation property: Translation
Invariance -
Dilation
and erosion have the following important properties. For any
arbitrary structuring element B and two image objects A1
and A2 such that A1
Increasing
in A -
For
two structuring elements B1 and B2
such that B1
Decreasing
in B -
The
decomposition theorems below make it possible to find
efficient implementations for morphological filters. Dilation
-
Erosion
-
Erosion
-
Multiple
Dilations -
An
important decomposition theorem is due to Vincent . First, we require
some definitions. A convex set (in R2) is one
for which the straight line joining any two points in the set consists
of points that are also in the set. Care must obviously be taken when
applying this definition to discrete pixels as the concept of a
"straight line" must be interpreted appropriately in Z2.
A set is bounded if each of its elements has a finite magnitude,
in this case distance to the origin of the coordinate system. A set is symmetric
if B = -B. The sets N4
and N8 in Figure 38 are examples of convex,
bounded, symmetric sets. Vincent's
theorem, when applied to an image consisting of discrete pixels, states
that for a bounded, symmetric structuring element B that
contains no holes and contains its own center,
where
*
Dilation - Take each binary object pixel (with value "1") and set all
background pixels (with value "0") that are C-connected
to that object pixel to the value "1". *
Erosion - Take each binary object pixel (with value "1") that is C-connected
to a background pixel and set the object pixel value to "0". Comparison
of these two procedures to eq. where B = NC=4
or NC=8 shows that they are equivalent to the
formal definitions for dilation and erosion. The procedure is
illustrated for dilation in Figure 39.
(a)
B = N4
(b) B= N8 Figure
39:
Illustration of dilation. Original object pixels are in gray;
pixels added through dilation are in black. Boolean Convolution
An arbitrary binary image
object (or structuring element) A can be represented as:
where
and
d[m,n]
is a Boolean version of the Dirac delta function that takes on the
Boolean values "1" and "0" as follows:
Dilation
for binary images can therefore be written as:
which,
because Boolean OR and AND are commutative, can also be
written as
Using
De Morgan's theorem:
on
eq. together with eq. , erosion can be written as:
Thus,
dilation and erosion on binary images can be viewed as a
form of convolution over a Boolean algebra. In
Section 9.3.2 we saw that, when convolution is employed, an appropriate
choice of the boundary conditions for an image is essential. Dilation
and erosion--being a Boolean convolution--are no exception. The two most
common choices are that either everything outside the binary image is
"0" or everything outside the binary image is "1". Opening and Closing
We can combine dilation
and erosion to build two important higher order operations: Opening
-
Closing
-
The
opening and closing have the following properties: Duality
-
Translation
-
For
the opening with structuring element B and images A,
A1, and A2, where A1
is a subimage of A2 (A1
Antiextensivity
-
Increasing
monotonicity -
Idempotence
-
For
the closing with structuring element B and images A,
A1, and A2, where A1
is a subimage of A2 (A1
Extensivity
-
Increasing
monotonicity -
Idempotence
-
The
two properties given by eqs. and are so important to mathematical
morphology that they can be considered as the reason for defining erosion
with -B instead of B in eq. . itandMiss operation
The hit-or-miss
operator was defined by Serra but we shall refer to it as the hit-and-miss
operator and define it as follows. Given an image A and
two structuring elements B1 and B2,
the set definition and Boolean definition are: Hit-and-Miss
-
where
B1 and B2 are bounded,
disjoint structuring elements. (Note the use of the notation from eq.
(81).) Two sets are disjoint if B1
Summary of the basic operations
The results of the application
of these basic operations on a test image are illustrated below. In
Figure 40 the various structuring elements used in the processing are
defined. The value "-" indicates a "don't care". All
three structuring elements are symmetric.
(a)
(b) (c) Figure 40:
Structuring elements B, B1, and B2
that are 3 x
3 and symmetric. The
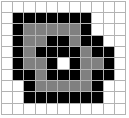
results of processing are shown in Figure 41 where the binary value
"1" is shown in black and the value "0" in white.
a)
Image A b) Dilation with 2B c)
Erosion with 2B
d)
Opening with 2B e) Closing with 2B
f) it-and-Miss with B1 and B2
Figure
41: Examples of various mathematical
morphology operations. The
opening operation can separate objects that are connected in a
binary image. The closing operation can fill in small holes. Both
operations generate a certain amount of smoothing on an object contour
given a "smooth" structuring element. The opening
smoothes from the inside of the object contour and the closing
smoothes from the outside of the object contour. The hit-and-miss
example has found the 4-connected contour pixels. An alternative method
to find the contour is simply to use the relation: 4-connected
contour -
or
8-connected
contour -
Skeleton
The informal definition of a
skeleton is a line representation of an object that is: i)
one-pixel thick, ii)
through the "middle" of the object, and, iii)
preserves the topology of the object. These
are not always realizable. Figure 42 shows why this is the case.
(a)
(b) Figure 42:
Counterexamples to the three requirements. In
the first example, Figure 42a, it is not possible to generate a line
that is one pixel thick and in the center of an object while generating
a path that reflects the simplicity of the object. In Figure 42b it is
not possible to remove a pixel from the 8-connected object and
simultaneously preserve the topology--the notion of connectedness--of
the object. Nevertheless, there are a variety of techniques that attempt
to achieve this goal and to produce a skeleton. A
basic formulation is based on the work of Lantuéjoul . The skeleton
subset Sk(A) is
defined as: Skeleton
subsets -
where
K is the largest value of k before the set Sk(A)
becomes empty. (From eq. ,
Skeleton
-
An
elegant side effect of this formulation is that the original object can
be reconstructed given knowledge of the skeleton subsets Sk(A),
the structuring element B, and K: Reconstruction
-
This
formulation for the skeleton, however, does not preserve the topology, a
requirement described in eq. . An
alternative point-of-view is to implement a thinning, an erosion
that reduces the thickness of an object without permitting it to vanish.
A general thinning algorithm is based on the hit-and-miss
operation: Thinning
-
Depending
on the choice of B1 and B2,
a large variety of thinning algorithms--and through repeated application
skeletonizing algorithms--can be implemented. A
quite practical implementation can be described in another way. If we
restrict ourselves to a 3 x 3 neighborhood, similar to the structuring element B
= N8 in Figure 40a, then we can view the thinning
operation as a window that repeatedly scans over the (binary) image and
sets the center pixel to "0" under certain conditions. The
center pixel is not changed to "0" if and only if: i)
an isolated pixel is found (e.g. Figure 43a), ii)
removing a pixel would change the connectivity (e.g. Figure 43b), iii)
removing a pixel would shorten a line (e.g. Figure 43c). As
pixels are (potentially) removed in each iteration, the process is
called a conditional erosion. Three test cases of eq. are
illustrated in Figure 43. In general all possible rotations and
variations have to be checked. As there are only 512 possible
combinations for a 3 x
3 window on a binary image, this can be done easily with the use of a
lookup table.
Figure 43:
Test conditions for conditional erosion of the center
pixel. If
only condition (i) is used then each object will be reduced to a
single pixel. This is useful if we wish to count the number of objects
in an image. If only condition (ii) is used then holes in the
objects will be found. If conditions (i + ii) are used
each object will be reduced to either a single pixel if it does not
contain a hole or to closed rings if it does contain holes. If
conditions (i + ii + iii) are used then the
"complete skeleton" will be generated as an approximation to
eq. . Illustrations of these various possibilities are given in Figure
44a,b. Propagation
It is convenient to be able to
reconstruct an image that has "survived" several erosions or
to fill an object that is defined, for example, by a boundary. The
formal mechanism for this has several names including region-filling,
reconstruction, and propagation. The formal definition is
given by the following algorithm. We start with a seed image S(0),
a mask image A, and a structuring element B.
We then use dilations of S with structuring element B
and masked by A in an iterative procedure as follows: Iteration
k -
With
each iteration the seed image grows (through dilation) but within
the set (object) defined by A; S propagates
to fill A. The most common choices for B are
N4 or N8. Several
remarks are central to the use of propagation. First, in a
straightforward implementation, as suggested by eq. , the computational
costs are extremely high. Each iteration requires O(N2)
operations for an N x N image and with the required number of
iterations this can lead to a complexity of O(N3).
Fortunately, a recursive implementation of the algorithm exists in which
one or two passes through the image are usually sufficient, meaning a
complexity of O(N2). Second, although we have
not paid much attention to the issue of object/background connectivity
until now (see Figure 36), it is essential that the connectivity implied
by B be matched to the connectivity associated with the
boundary definition of A (see eqs. and ). Finally, as
mentioned earlier, it is important to make the correct choice
("0" or "1") for the boundary condition of the
image. The choice depends upon the application. Summary of skeleton and propagation
The application of these two
operations on a test image is illustrated in Figure 44. In Figure 44a,b
the skeleton operation is shown with the endpixel condition (eq. i+ii+iii)
and without the end pixel condition (eq. i+ii). The
propagation operation is illustrated in Figure 44c. The original image,
shown in light gray, was eroded by E(A,6N8)
to produce the seed image shown in black. The original was then
used as the mask image to produce the final result. The border
value in both images was "0". Several
techniques based upon the use of skeleton and propagation
operations in combination with other mathematical morphology operations
will be given in Section 10.3.3.
Original
= light gray Mask = light gray
a)
Skeleton with end pixels b) Skeleton without end
pixels c) Propagation with N8 Condition
eq. i+ii+iii Condition eq. i+ii Figure
44: Examples of skeleton and propagation.
Gray-value morphological processing
The techniques of morphological
filtering can be extended to gray-level images. To simplify matters we
will restrict our presentation to structuring elements, B,
that comprise a finite number of pixels and are convex and bounded. Now,
however, the structuring element has gray values associated with every
coordinate position as does the image A. *
Gray-level dilation, DG(*), is given by: Dilation
-
For
a given output coordinate [m,n], the structuring element
is summed with a shifted version of the image and the maximum
encountered over all shifts within the J x K domain of B is used as
the result. Should the shifting require values of the image A
that are outside the M x N domain of A, then
a decision must be made as to which model for image extension, as
described in Section 9.3.2, should be used. *
Gray-level erosion, EG(*), is given by: Erosion
-
The
duality between gray-level erosion and gray-level dilation--the
gray-level counterpart of eq. --is somewhat more complex than in the
binary case: Duality
-
where
"
The
definitions of higher order operations such as gray-level opening
and gray-level closing are: Opening
-
Closing
-
The
important properties that were discussed earlier such as idempotence,
translation invariance, increasing in A, and so forth are also
applicable to gray level morphological processing. The details can be
found in Giardina and Dougherty . In
many situations the seeming complexity of gray level morphological
processing is significantly reduced through the use of symmetric
structuring elements where b[j,k] = b[-j,-k].
The most common of these is based on the use of B = constant
= 0. For this important case and using again the domain [j,k]
Dilation
-
Erosion
-
Opening
-
Closing
-
The
remarkable conclusion is that the maximum filter and the minimum
filter, introduced in Section 9.4.2, are gray-level dilation and
gray-level erosion for the specific structuring element given by the
shape of the filter window with the gray value "0" inside
the window. Examples of these operations on a simple one-dimensional
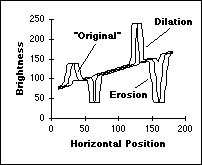
signal are shown in Figure 45.
a)
Effect of 15 x 1 dilation
and erosion b) Effect of 15 x 1 opening and
closing Figure 45:
Morphological filtering of gray-level data. For
a rectangular window, J x K, the two-dimensional maximum or minimum
filter is separable into two, one-dimensional windows. Further, a
one-dimensional maximum or minimum filter can be written in incremental
form. (See Section 9.3.2.) This means that gray-level dilations and
erosions have a computational complexity per pixel that is O(constant),
that is, independent of J and K. (See also Table 13.) The
operations defined above can be used to produce morphological algorithms
for smoothing, gradient determination and a version of the Laplacian.
All are constructed from the primitives for gray-level dilation
and gray-level erosion and in all cases the maximum
and minimum filters are taken over the domain
Morphological smoothing
This algorithm is based on the
observation that a gray-level opening smoothes a
gray-value image from above the brightness surface given by the function
a[m,n] and the gray-level closing
smoothes from below. We use a structuring element B based
on eqs. and .
Note
that we have suppressed the notation for the structuring element B
under the max and min operations to keep the notation
simple. Its use, however, is understood. Morphological gradient
For linear filters the gradient
filter yields a vector representation (eq. (103)) with a magnitude (eq.
(104)) and direction (eq. (105)). The version presented here generates a
morphological estimate of the gradient magnitude:
Morphological Laplacian
The morphologically-based
Laplacian filter is defined by:
Summary of morphological filters
The effect of these filters is
illustrated in Figure 46. All images were processed with a 3 x
3 structuring element as described in eqs. through . Figure 46e was
contrast stretched for display purposes using eq. (78) and the
parameters 1% and 99%. Figures 46c,d,e should be compared to Figures 30,
32, and 33.
a)
Dilation b) Erosion c) Smoothing
d)
Gradient e) Laplacian Figure 46:
Examples of gray-level morphological filters. |





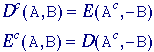

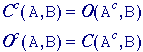
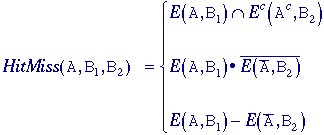


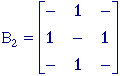
 d)
d)