The
algorithms presented in Section 9 can be used to build techniques to
solve specific image processing problems. Without presuming to present
the solution to all processing problems, the following examples are of
general interest and can be used as models for solving related problems.


The
method by which images are produced--the interaction between objects in
real space, the illumination, and the camera--frequently leads to
situations where the image exhibits significant shading across the
field-of-view. In some cases the image might be bright in the center and
decrease in brightness as one goes to the edge of the field-of-view. In
other cases the image might be darker on the left side and lighter on
the right side. The shading might be caused by non-uniform illumination,
non-uniform camera sensitivity, or even dirt and dust on glass (lens)
surfaces. In general this shading effect is undesirable. Eliminating it
is frequently necessary for subsequent processing and especially when
image analysis or image understanding is the final goal.
In general we begin with a model
for the shading effect. The illumination Iill(x,y)
usually interacts in a multiplicative with the object a(x,y)
to produce the image b(x,y):
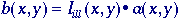
with
the object representing various imaging modalities such as:

where
at position (x,y), r(x,y) is the reflectance,
OD(x,y) is the optical density, and c(x,y)
is the concentration of fluorescent material. Parenthetically, we note
that the fluorescence model only holds for low concentrations. The
camera may then contribute gain and offset terms, as in eq.
(74), so that:
Total
shading -
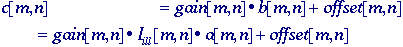
In
general we assume that Iill[m,n] is
slowly varying compared to a[m,n].
We distinguish between two cases
for the determination of a[m,n] starting from c[m,n].
In both cases we intend to estimate the shading terms {gain[m,n]*Iill[m,n]}
and {offset[m,n]}. While in the first case we
assume that we have only the recorded image c[m,n]
with which to work, in the second case we assume that we can record two,
additional, calibration images.
*
A posteriori estimate - In this case we attempt to extract the
shading estimate from c[m,n]. The most common
possibilities are the following.
Lowpass
filtering - We compute a smoothed version of c[m,n] where the
smoothing is large compared to the size of the objects in the image.
This smoothed version is intended to be an estimate of the background of
the image. We then subtract the smoothed version from c[m,n]
and then restore the desired DC value. In formula:
Lowpass
-
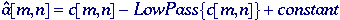
where
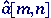 is the
estimate of a[m,n]. Choosing the appropriate
lowpass filter means knowing the appropriate spatial frequencies in the
Fourier domain where the shading terms dominate. is the
estimate of a[m,n]. Choosing the appropriate
lowpass filter means knowing the appropriate spatial frequencies in the
Fourier domain where the shading terms dominate.
omomorphic
filtering - We note that, if the offset[m,n] = 0, then c[m,n]
consists solely of multiplicative terms. Further, the term {gain[m,n]*Iill[m,n]}
is slowly varying while a[m,n] presumably is not.
We therefore take the logarithm of c[m,n] to
produce two terms one of which is low frequency and one of which is high
frequency. We suppress the shading by high pass filtering the logarithm
of c[m,n] and then take the exponent (inverse
logarithm) to restore the image. This procedure is based on homomorphic
filtering as developed by Oppenheim, Schafer and Stockham . In
formula:
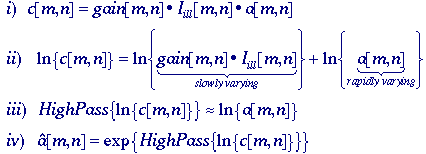
Morphological
filtering - We again compute a smoothed version of c[m,n]
where the smoothing is large compared to the size of the objects in the
image but this time using morphological smoothing as in eq. . This
smoothed version is the estimate of the background of the image. We then
subtract the smoothed version from c[m,n] and then
restore the desired DC value. In formula:

Choosing
the appropriate morphological filter window means knowing (or
estimating) the size of the largest objects of interest.
*
A priori estimate - If it is possible to record test (calibration) images through the
cameras system, then the most appropriate technique for the removal of
shading effects is to record two images - BLACK[m,n]
and WHITE[m,n]. The BLACK image is generated
by covering the lens leading to b[m,n] = 0 which in
turn leads to BLACK[m,n] = offset[m,n].
The WHITE image is generated by using a[m,n]
= 1 which gives WHITE[m,n] = gain[m,n]*Iill[m,n]
+ offset[m,n]. The correction then becomes:

The
constant term is chosen to produce the desired dynamic range.
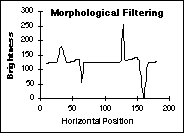
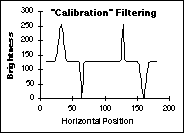
The
effects of these various techniques on the data from Figure 45 are shown
in Figure 47. The shading is a simple, linear ramp increasing from left
to right; the objects consist of Gaussian peaks of varying widths.
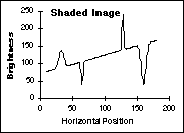 (a)
Original (a)
Original
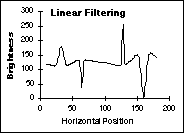
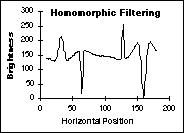
(b)
Correction with Lowpass filtering (c) Correction with Logarithmic
filtering
(c)
Correction with Max/Min filtering (d) Correction with Test Images
Figure
47:
Comparison of various shading correction algorithms. The final result
(d) is identical to the original (not shown).
In
summary, if it is possible to obtain BLACK and WHITE
calibration images, then eq. is to be preferred. If this is not
possible, then one of the other algorithms will be necessary.
The
process of image acquisition frequently leads (inadvertently) to image
degradation. Due to mechanical problems, out-of-focus blur, motion,
inappropriate illumination, and noise the quality of the digitized image
can be inferior to the original. The goal of enhancement is--
starting from a recorded image c[m,n]--to produce
the most visually pleasing image â[m,n]. The
goal of restoration is--starting from a recorded image c[m,n]--to
produce the best possible estimate â[m,n] of
the original image a[m,n]. The goal of enhancement
is beauty; the goal of restoration is truth.
The
measure of success in restoration is usually an error measure between
the original a[m,n] and the estimate â[m,n]:
E{â[m,n], a[m,n]}. No
mathematical error function is known that corresponds to human
perceptual assessment of error. The mean-square error function is
commonly used because:
1.
It is easy to compute;
2.
It is differentiable implying that a minimum can be sought;
3.
It corresponds to "signal energy" in the total error, and;
4.
It has nice properties vis ¨¤ vis Parseval's
theorem, eqs. (22) and (23).
The
mean-square error is defined by:
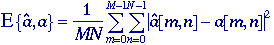
In
some techniques an error measure will not be necessary; in others it
will be essential for evaluation and comparative purposes.
A well-known technique from
photography to improve the visual quality of an image is to enhance the
edges of the image. The technique is called unsharp masking.
Edge enhancement means first isolating the edges in an image, amplifying
them, and then adding them back into the image. Examination of Figure 33
shows that the Laplacian is a mechanism for isolating the gray level
edges. This leads immediately to the technique:

The
term k is the amplifying term and k > 0. The effect of
this technique is shown in Figure 48.
The
Laplacian used to produce Figure 48 is given by eq. (120) and the
amplification term k = 1.

Original

 Laplacian-enhanced Laplacian-enhanced
Figure
48: Edge enhanced compared to original
The techniques available to
suppress noise can be divided into those techniques that are based on
temporal information and those that are based on spatial information. By
temporal information we mean that a sequence of images {ap[m,n]
| p=1,2,...,P} are available that contain exactly
the same objects and that differ only in the sense of independent noise
realizations. If this is the case and if the noise is additive, then
simple averaging of the sequence:
Temporal
averaging -
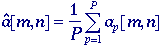
will
produce a result where the mean value of each pixel will be unchanged.
For each pixel, however, the standard deviation will decrease from
 to to
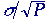 . .
If
temporal averaging is not possible, then spatial averaging can be used
to decrease the noise. This generally occurs, however, at a cost to
image sharpness. Four obvious choices for spatial averaging are the
smoothing algorithms that have been described in Section 9.4 - Gaussian
filtering (eq. (93)), median filtering, Kuwahara filtering, and
morphological smoothing (eq. ).
Within
the class of linear filters, the optimal filter for restoration in the
presence of noise is given by the Wiener filter . The word
"optimal" is used here in the sense of minimum mean-square
error (mse). Because the square root operation is monotonic
increasing, the optimal filter also minimizes the root mean-square error
(rms). The Wiener filter is characterized in the Fourier domain
and for additive noise that is independent of the signal it is given by:
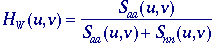
where
Saa(u,v) is the power spectral density
of an ensemble of random images {a[m,n]} and Snn(u,v)
is the power spectral density of the random noise. If we have a single
image then Saa(u,v) = |A(u,v)|2.
In practice it is unlikely that the power spectral density of the
uncontaminated image will be available. Because many images have a
similar power spectral density that can be modeled by Table 4-T.8, that
model can be used as an estimate of Saa(u,v).
A
comparison of the five different techniques described above is shown in
Figure 49. The Wiener filter was constructed directly from eq. because
the image spectrum and the noise spectrum were known. The parameters for
the other filters were determined choosing that value (either
 or window size) that led to the minimum rms. or window size) that led to the minimum rms.



a)
Noisy image (SNR=20 dB) b) Wiener filter c)
Gauss filter (
 = 1.0) = 1.0)
rms
= 25.7 rms = 20.2 rms = 21.1



d)
Kuwahara filter (5 x
5) e) Median filter (3 x 3) f) Morph. smoothing (3 x
3)
rms
= 22.4 rms = 22.6 rms = 26.2
Figure
49: Noise suppression using various
filtering techniques.
The
root mean-square errors (rms) associated with the various filters
are shown in Figure 49. For this specific comparison, the Wiener filter
generates a lower error than any of the other procedures that are
examined here. The two linear procedures, Wiener filtering and Gaussian
filtering, performed slightly better than the three non-linear
alternatives.
The model presented above--an
image distorted solely by noise--is not, in general, sophisticated
enough to describe the true nature of distortion in a digital image. A
more realistic model includes not only the noise but also a model for
the distortion induced by lenses, finite apertures, possible motion of
the camera and/or an object, and so forth. One frequently used model is
of an image a[m,n] distorted by a linear,
shift-invariant system ho[m,n] (such as
a lens) and then contaminated by noise
 [m,n].
Various aspects of ho[m,n] and [m,n].
Various aspects of ho[m,n] and
 [m,n]
have been discussed in earlier sections. The most common combination of
these is the additive model: [m,n]
have been discussed in earlier sections. The most common combination of
these is the additive model:

The
restoration procedure that is based on linear filtering coupled to a
minimum mean-square error criterion again produces a Wiener filter :
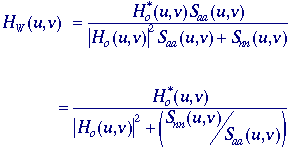
Once
again Saa(u,v) is the power spectral
density of an image, Snn(u,v) is the
power spectral density of the noise, and o(u,v)
= F{ho[m,n]}. Examination of this
formula for some extreme cases can be useful. For those frequencies
where Saa(u,v) >> Snn(u,v),
where the signal spectrum dominates the noise spectrum, the Wiener
filter is given by 1/o(u,v), the inverse
filter solution. For those frequencies where Saa(u,v)
<< Snn(u,v), where the noise
spectrum dominates the signal spectrum, the Wiener filter is
proportional to o*(u,v), the matched
filter solution. For those frequencies where o(u,v)
= 0, the Wiener filter W(u,v) = 0
preventing overflow.
The
Wiener filter is a solution to the restoration problem based upon the
hypothesized use of a linear filter and the minimum mean-square (or rms)
error criterion. In the example below the image a[m,n]
was distorted by a bandpass filter and then white noise was added to
achieve an SNR = 30 dB. The results are shown in Figure
50.



a)
Distorted, noisy image b) Wiener filter c) Median filter
(3 x 3)
rms
= 108.4 rms = 40.9 Figure 50: Noise and distortion
suppression using the Wiener filter, eq. and the median filter.
The
rms after Wiener filtering but before contrast stretching was
108.4; after contrast stretching with eq. (77) the final result as shown
in Figure 50b has a mean-square error of 27.8. Using a 3 x
3 median filter as shown in Figure 50c leads to a rms
error of 40.9 before contrast stretching and 35.1 after contrast
stretching. Although the Wiener filter gives the minimum rms
error over the set of all linear filters, the non-linear
median filter gives a lower rms error. The operation contrast
stretching is itself a non-linear operation. The "visual
quality" of the median filtering result is comparable to the Wiener
filtering result. This is due in part to periodic artifacts introduced
by the linear filter which are visible in Figure 50b.

In
the analysis of the objects in images it is essential that we can
distinguish between the objects of interest and "the rest."
This latter group is also referred to as the background. The techniques
that are used to find the objects of interest are usually referred to as
segmentation techniques - segmenting the foreground from
background. In this section we will two of the most common techniques--thresholding
and edge finding-- and we will present techniques for
improving the quality of the segmentation result. It is important to
understand that:
*
there
is no universally applicable segmentation technique that will work for
all images, and,
*
no
segmentation technique is perfect.
This technique is based upon a
simple concept. A parameter
 called
the brightness threshold is chosen and applied to the
image a[m,n] as follows: called
the brightness threshold is chosen and applied to the
image a[m,n] as follows:
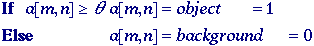
This
version of the algorithm assumes that we are interested in light objects
on a dark background. For dark objects on a light background we would
use:
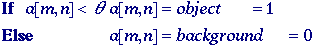
The
output is the label "object" or "background" which,
due to its dichotomous nature, can be represented as a Boolean variable
"1" or "0". In principle, the test condition could
be based upon some other property than simple brightness (for example, If
(Redness{a[m,n]} >=
 red),
but the concept is clear. red),
but the concept is clear.
The
central question in thresholding then becomes: ow do we choose the
threshold
 ? While there is no universal procedure for
threshold selection that is guaranteed to work on all images, there are
a variety of alternatives. ? While there is no universal procedure for
threshold selection that is guaranteed to work on all images, there are
a variety of alternatives.
*
Fixed threshold - One alternative is to use a threshold that is chosen independently of
the image data. If it is known that one is dealing with very
high-contrast images where the objects are very dark and the background
is homogeneous (Section 10.1) and very light, then a constant threshold
of 128 on a scale of 0 to 255 might be sufficiently accurate. By
accuracy we mean that the number of falsely-classified pixels should be
kept to a minimum.
*
Histogram-derived thresholds - In most cases the threshold is chosen from the
brightness histogram of the region or image that we wish to segment.
(See Sections 3.5.2 and 9.1.) An image and its associated brightness
histogram are shown in Figure 51.
A
variety of techniques have been devised to automatically choose a
threshold starting from the gray-value histogram, {h[b] | b
= 0, 1, ... , 2B-1}. Some of the most common ones are
presented below. Many of these algorithms can benefit from a smoothing
of the raw histogram data to remove small fluctuations but the smoothing
algorithm must not shift the peak positions. This translates into a
zero-phase smoothing algorithm given below where typical values for W
are 3 or 5:
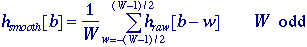


(a)
Image to be thresholded (b) Brightness histogram of the
image
Figure
51:
Pixels below the threshold (a[m,n] <
 ) will be labeled as object pixels; those
above the threshold will be labeled as background pixels. ) will be labeled as object pixels; those
above the threshold will be labeled as background pixels.
*
Isodata algorithm - This iterative technique for choosing a threshold
was developed by Ridler and Calvard . The histogram is initially
segmented into two parts using a starting threshold value such as
 0
= 2B-1, half the maximum dynamic range. The
sample mean (mf,0) of the gray values associated with
the foreground pixels and the sample mean (mb,0) of
the gray values associated with the background pixels are computed. A
new threshold value 0
= 2B-1, half the maximum dynamic range. The
sample mean (mf,0) of the gray values associated with
the foreground pixels and the sample mean (mb,0) of
the gray values associated with the background pixels are computed. A
new threshold value
 1
is now computed as the average of these two sample means. The process is
repeated, based upon the new threshold, until the threshold value does
not change any more. In formula: 1
is now computed as the average of these two sample means. The process is
repeated, based upon the new threshold, until the threshold value does
not change any more. In formula:
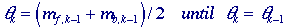
*
Background-symmetry algorithm - This technique assumes a distinct and
dominant peak for the background that is symmetric about its maximum.
The technique can benefit from smoothing as described in eq. . The
maximum peak (maxp) is found by searching for the maximum value
in the histogram. The algorithm then searches on the non-object pixel
side of that maximum to find a p% point as in eq. (39).
In
Figure 51b, where the object pixels are located to the left of
the background peak at brightness 183, this means searching to the right
of that peak to locate, as an example, the 95% value. At this brightness
value, 5% of the pixels lie to the right (are above) that value.
This occurs at brightness 216 in Figure 51b. Because of the assumed
symmetry, we use as a threshold a displacement to the left of the
maximum that is equal to the displacement to the right where the p%
is found. For Figure 51b this means a threshold value given by 183 -
(216 - 183) = 150. In formula:

This
technique can be adapted easily to the case where we have light objects
on a dark, dominant background. Further, it can be used if the object
peak dominates and we have reason to assume that the brightness
distribution around the object peak is symmetric. An additional
variation on this symmetry theme is to use an estimate of the sample
standard deviation (s in eq. (37)) based on one side of the
dominant peak and then use a threshold based on
 = maxp +/- 1.96s (at the 5%
level) or = maxp +/- 1.96s (at the 5%
level) or
 = maxp +/- 2.57s (at the 1%
level). The choice of "+" or "-" depends on which
direction from maxp is being defined as the object/background
threshold. Should the distributions be approximately Gaussian around maxp,
then the values 1.96 and 2.57 will, in fact, correspond to the 5% and 1
% level. = maxp +/- 2.57s (at the 1%
level). The choice of "+" or "-" depends on which
direction from maxp is being defined as the object/background
threshold. Should the distributions be approximately Gaussian around maxp,
then the values 1.96 and 2.57 will, in fact, correspond to the 5% and 1
% level.
*
Triangle algorithm - This technique due to Zack [36] is illustrated in
Figure 52. A line is constructed between the maximum of the histogram at
brightness bmax and the lowest value bmin
= (p=0)% in the image. The distance d between the line and
the histogram h[b] is computed for all values of b
from b = bmin to b = bmax.
The brightness value bo where the distance between h[bo]
and the line is maximal is the threshold value, that is,
 = bo. This technique is
particularly effective when the object pixels produce a weak peak in the
histogram. = bo. This technique is
particularly effective when the object pixels produce a weak peak in the
histogram.
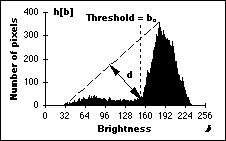
Figure 52:
The triangle algorithm is based on finding the value of b that
gives the maximum distance d.
The
three procedures described above give the values
 = 139 for the Isodata algorithm, = 139 for the Isodata algorithm,
 = 150 for the background symmetry algorithm at
the 5% level, and = 150 for the background symmetry algorithm at
the 5% level, and
 = 152 for the triangle algorithm for the image
in Figure 51a. = 152 for the triangle algorithm for the image
in Figure 51a.
Thresholding
does not have to be applied to entire images but can be used on a region
by region basis. Chow and Kaneko developed a variation in which the M
x
N image is divided into non-overlapping regions. In each region a
threshold is calculated and the resulting threshold values are put
together (interpolated) to form a thresholding surface for the entire
image. The regions should be of "reasonable" size so that
there are a sufficient number of pixels in each region to make an
estimate of the histogram and the threshold. The utility of this
procedure--like so many others--depends on the application at hand.
Thresholding produces a
segmentation that yields all the pixels that, in principle, belong to
the object or objects of interest in an image. An alternative to this is
to find those pixels that belong to the borders of the objects.
Techniques that are directed to this goal are termed edge finding
techniques. From our discussion in Section 9.6 on mathematical
morphology, specifically eqs. , , and , we see that there is an intimate
relationship between edges and regions.
*
Gradient-based procedure - The central challenge to edge finding techniques is
to find procedures that produce closed contours around the
objects of interest. For objects of particularly high SNR, this
can be achieved by calculating the gradient and then using a suitable
threshold. This is illustrated in Figure 53.


 (a)
SNR = 30 dB (b) SNR = 20 dB (a)
SNR = 30 dB (b) SNR = 20 dB
Figure
53:
Edge finding based on the Sobel gradient, eq. (110), combined with the
Isodata thresholding algorithm eq. .
While
the technique works well for the 30 dB image in Figure 53a, it fails to
provide an accurate determination of those pixels associated with the
object edges for the 20 dB image in Figure 53b. A variety of smoothing
techniques as described in Section 9.4 and in eq. can be used to reduce
the noise effects before the gradient operator is applied.
*
Zero-crossing based procedure - A more modern view to handling the problem
of edges in noisy images is to use the zero crossings generated in the
Laplacian of an image (Section 9.5.2). The rationale starts from the
model of an ideal edge, a step function, that has been blurred by an OTF
such as Table 4 T.3 (out-of-focus), T.5 (diffraction-limited), or T.6
(general model) to produce the result shown in Figure 54.
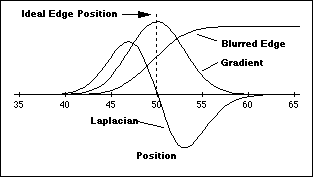
Figure 54:
Edge finding based on the zero crossing as determined by the second
derivative, the Laplacian. The curves are not to scale.
The
edge location is, according to the model, at that place in the image
where the Laplacian changes sign, the zero crossing. As the Laplacian
operation involves a second derivative, this means a potential
enhancement of noise in the image at high spatial frequencies; see eq.
(114). To prevent enhanced noise from dominating the search for zero
crossings, a smoothing is necessary.
The
appropriate smoothing filter, from among the many possibilities
described in Section 9.4, should according to Canny have the following
properties:
*
In the frequency domain, (u,v) or (
 , ,
 ), the filter should be as narrow as possible
to provide suppression of high frequency noise, and; ), the filter should be as narrow as possible
to provide suppression of high frequency noise, and;
*
In the spatial domain, (x,y) or [m,n], the
filter should be as narrow as possible to provide good localization of
the edge. A too wide filter generates uncertainty as to precisely where,
within the filter width, the edge is located.
The
smoothing filter that simultaneously satisfies both these
properties--minimum bandwidth and minimum spatial width--is the Gaussian
filter described in Section 9.4. This means that the image should be
smoothed with a Gaussian of an appropriate
 followed by application of the Laplacian. In
formula: followed by application of the Laplacian. In
formula:
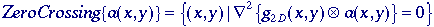
where
g2D(x,y) is defined in eq. (93). The
derivative operation is linear and shift-invariant as defined in eqs.
(85) and (86). This means that the order of the operators can be
exchanged (eq. (4)) or combined into one single filter (eq. (5)). This
second approach leads to the Marr-ildreth formulation of the "Laplacian-of-Gaussians"
(LoG) filter :
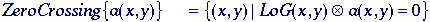
where
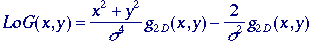
Given
the circular symmetry this can also be written as:

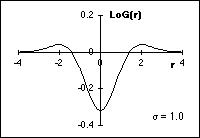
This
two-dimensional convolution kernel, which is sometimes referred to as a
"Mexican hat filter", is illustrated in Figure 55.

(a)
-LoG(x,y)
(b) LoG(r)
Figure
55: LoG filter with
 =
1.0. =
1.0.
*PLUS-based
procedure - Among the zero crossing procedures for edge detection, perhaps the
most accurate is the PLUS filter as developed by Verbeek and Van
Vliet . The filter is defined, using eqs. (121) and (122), as:
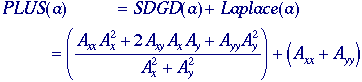
Neither
the derivation of the PLUS's properties nor an evaluation of its
accuracy are within the scope of this section. Suffice it to say that,
for positively curved edges in gray value images, the Laplacian-based
zero crossing procedure overestimates the position of the edge
and the SDGD-based procedure underestimates the position.
This is true in both two-dimensional and three-dimensional images with
an error on the order of (
 /R)2 where R is the
radius of curvature of the edge. The PLUS operator has an error
on the order of ( /R)2 where R is the
radius of curvature of the edge. The PLUS operator has an error
on the order of (
 /R)4 if the image is sampled
at, at least, 3x the usual Nyquist sampling frequency as in eq. (56) or
if we choose /R)4 if the image is sampled
at, at least, 3x the usual Nyquist sampling frequency as in eq. (56) or
if we choose
 >= 2.7 and sample at the usual Nyquist
frequency. >= 2.7 and sample at the usual Nyquist
frequency.
All
of the methods based on zero crossings in the Laplacian must be able to
distinguish between zero crossings and zero values. While
the former represent edge positions, the latter can be generated by
regions that are no more complex than bilinear surfaces, that is, a(x,y)
= a0 + a1*x + a2*y
+ a3*x*y. To distinguish between these
two situations, we first find the zero crossing positions and label them
as "1" and all other pixels as "0". We then multiply
the resulting image by a measure of the edge strength at
each pixel. There are various measures for the edge strength that are
all based on the gradient as described in Section 9.5.1 and eq. . This
last possibility, use of a morphological gradient as an edge strength
measure, was first described by Lee, aralick, and Shapiro and is
particularly effective. After multiplication the image is then
thresholded (as above) to produce the final result. The procedure is
thus as follows :
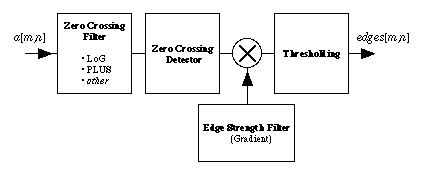
Figure
56: General strategy for edges based on zero crossings.
The
results of these two edge finding techniques based on zero crossings, LoG
filtering and PLUS filtering, are shown in Figure 57 for images
with a 20 dB SNR.



a)
Image SNR = 20 dB

 b)
LoG filter b)
LoG filter

 c)
PLUS filter c)
PLUS filter



Figure
57:
Edge finding using zero crossing algorithms LoG and PLUS.
In both algorithms
 = 1.5. = 1.5.
Edge
finding techniques provide, as the name suggests, an image that contains
a collection of edge pixels. Should the edge pixels correspond to
objects, as opposed to say simple lines in the image, then a
region-filling technique such as eq. may be required to provide the
complete objects.
The various algorithms that we
have described for mathematical morphology in Section 9.6 can be put
together to form powerful techniques for the processing of binary images
and gray level images. As binary images frequently result from
segmentation processes on gray level images, the morphological
processing of the binary result permits the improvement of the
segmentation result.
*
Salt-or-pepper filtering - Segmentation procedures frequently result in
isolated "1" pixels in a "0" neighborhood (salt) or
isolated "0" pixels in a "1" neighborhood (pepper).
The appropriate neighborhood definition must be chosen as in Figure 3.
Using the lookup table formulation for Boolean operations in a 3 x
3 neighborhood that was described in association with Figure 43, salt
filtering and pepper filtering are straightforward to
implement. We weight the different positions in the 3 x 3 neighborhood as follows:
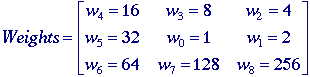
For
a 3 x
3 window in a[m,n] with values "0" or
"1" we then compute:
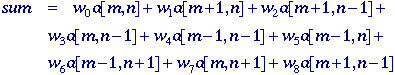
The
result, sum, is a number bounded by 0 <= sum <= 511.
*
Salt Filter - The 4-connected and 8-connected versions of this filter are the same
and are given by the following procedure:
i)
Compute sum ii) If ( (sum == 1) c[m,n]
= 0 Else c[m,n] = a[m,n]
*
Pepper Filter - The 4-connected and 8-connected versions of this filter are the
following procedures:
4-connected
8-connected i) Compute sum i)
Compute sum ii) If ( (sum == 170) ii) If ( (sum
== 510) c[m,n] = 1 c[m,n] = 1 Else
Else c[m,n] = a[m,n] c[m,n]
= a[m,n]
*
Isolate objects with holes - To find objects with holes we can use the following
procedure which is illustrated in Figure 58.
i)
Segment image to produce binary mask representation ii) Compute skeleton
without end pixels - eq. iii) Use salt filter
to remove single skeleton pixels iv) Propagate remaining skeleton
pixels into original binary mask - eq.



a)
Binary image b) Skeleton after salt filter c) Objects with
holes
Figure 58:
Isolation of objects with holes using morphological operations.
The
binary objects are shown in gray and the skeletons, after application of
the salt filter, are shown as a black overlay on the binary objects.
Note that this procedure uses no parameters other then the fundamental
choice of connectivity; it is free from "magic numbers." In
the example shown in Figure 58, the 8-connected definition was used as
well as the structuring element B = N8.
*
Filling holes in objects - To fill holes in objects we use the following
procedure which is illustrated in Figure 59.
i)
Segment image to produce binary representation of objects ii)
Compute complement of binary image as a mask image
iii) Generate a seed image as the border of the image iv) Propagate
the seed into the mask - eq. v) Complement result
of propagation to produce final result

 a) Mask
and Seed images b) Objects with holes filled a) Mask
and Seed images b) Objects with holes filled
Figure 59:
Filling holes in objects.
The
mask image is illustrated in gray in Figure 59a and
the seed image is shown in black in that same
illustration. When the object pixels are specified with a connectivity
of C = 8, then the propagation into the mask (background) image
should be performed with a connectivity of C = 4, that is,
dilations with the structuring element B = N4.
This procedure is also free of "magic numbers."
*
Removing border-touching objects - Objects that are connected to the image
border are not suitable for analysis. To eliminate them we can use a
series of morphological operations that are illustrated in Figure 60.
i)
Segment image to produce binary mask image of
objects ii) Generate a seed image as the border of the
image iv) Propagate the seed into the mask - eq. v)
Compute XOR of the propagation result and the mask image
as final result

 a)
Mask and Seed images b) Remaining objects a)
Mask and Seed images b) Remaining objects
Figure 60:
Removing objects touching borders.
The
mask image is illustrated in gray in Figure 60a and
the seed image is shown in black in that same
illustration. If the structuring element used in the propagation is B
= N4, then objects are removed that are
4-connected with the image boundary. If B = N8
is used then objects that 8-connected with the boundary are removed.
*
Exo-skeleton - The exo-skeleton of a set of objects is the skeleton of the
background that contains the objects. The exo-skeleton produces a
partition of the image into regions each of which contains one object.
The actual skeletonization (eq. ) is performed without the preservation
of end pixels and with the border set to "0." The procedure is
described below and the result is illustrated in Figure 61.
i)
Segment image to produce binary image ii) Compute complement
of binary image iii) Compute skeleton using eq. i+ii with
border set to "0"
Figure 61:
Exo-skeleton.
*
Touching objects - Segmentation procedures frequently have difficulty
separating slightly touching, yet distinct, objects. The following
procedure provides a mechanism to separate these objects and makes
minimal use of "magic numbers." The exo-skeleton produces a
partition of the image into regions each of which contains one object.
The actual skeletonization is performed without the preservation of end
pixels and with the border set to "0." The procedure is
illustrated in Figure 62.
i)
Segment image to produce binary image ii) Compute a "small
number" of erosions with B = N4
iii) Compute exo-skeleton of eroded result iv) Complement exo-skeleton
result iii) Compute AND of original binary image and the
complemented exo-skeleton
 a)
Eroded and exo-skeleton images b) Objects separated (detail) a)
Eroded and exo-skeleton images b) Objects separated (detail)
Figure 62:
Separation of touching objects.
The
eroded binary image is illustrated in gray
in Figure 62a and the exo-skeleton image is shown in black
in that same illustration. An enlarged section of the final result is
shown in Figure 62b and the separation is easily seen. This procedure
involves choosing a small, minimum number of erosions but the number is
not critical as long as it initiates a coarse separation of the desired
objects. The actual separation is performed by the exo-skeleton which,
itself, is free of "magic numbers." If the exo-skeleton is
8-connected than the background separating the objects will be
8-connected. The objects, themselves, will be disconnected according to
the 4-connected criterion. (See Section 9.6 and Figure 36.)
As we have seen in Section
10.1.2, gray-value morphological processing techniques can be used for
practical problems such as shading correction. In this section several
other techniques will be presented.
*
Top-hat transform - The isolation of gray-value objects that are convex
can be accomplished with the top-hat transform as
developed by Meyer . Depending upon whether we are dealing with light
objects on a dark background or dark objects on a light background, the
transform is defined as:
Light
objects -

Dark
objects -
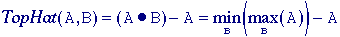
where
the structuring element B is chosen to be bigger than the
objects in question and, if possible, to have a convex shape. Because of
the properties given in eqs. and , Topat(A,B)
>= 0. An example of this technique is shown in Figure 63.
The
original image including shading is processed by a 15 x
1 structuring element as described in eqs. and to produce the desired
result. Note that the transform for dark objects has been defined in
such a way as to yield "positive" objects as opposed to
"negative" objects. Other definitions are, of course,
possible.
*
Thresholding - A simple estimate of a locally-varying threshold surface can be
derived from morphological processing as follows:
Threshold
surface -
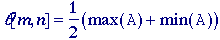
Once
again, we suppress the notation for the structuring element B
under the max and min operations to keep the notation
simple. Its use, however, is understood.
 (a)
Original (a)
Original


(a)
Light object transform (b) Dark object transform
Figure 63:
Top-hat transforms.
*
Local contrast stretching - Using morphological operations we can implement a
technique for local contrast stretching. That is,
the amount of stretching that will be applied in a neighborhood will be
controlled by the original contrast in that neighborhood. The
morphological gradient defined in eq. may also be seen as related to a
measure of the local contrast in the window defined by the structuring
element B:

The
procedure for local contrast stretching is given by:
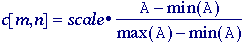
The
max and min operations are taken over the structuring
element B. The effect of this procedure is illustrated in
Figure 64. It is clear that this local operation is an extended
version of the point operation for contrast stretching presented
in eq. (77).



 before
after before
after

 before
after before
after

 before
after before
after

Figure 64:
Local contrast stretching.
Using standard test
images (as we have seen in so many examples) illustrates the power of
this local morphological filtering approach. |

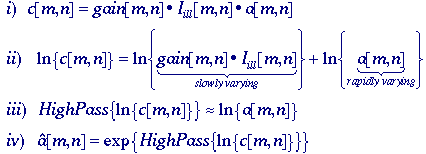
 (a)
Original
(a)
Original











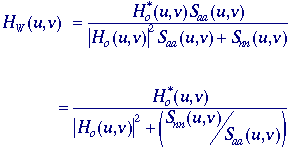









 (a)
(a)


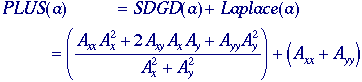





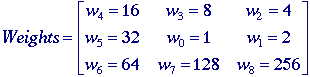
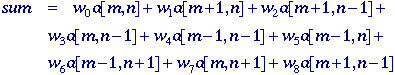




 a)
a) 
 a)
a)

 a)
a)



